Vzorec pro čas, rychlost a vzdálenost: 4. třída. Jak zjistit čas, znát rychlost a vzdálenost? Jak zjistit rychlost, pokud je znám čas a vzdálenost? Jak zjistit vzdálenost, pokud je znám čas a rychlost? Graf závislosti rychlosti těla na čase

Jak řešit pohybové úlohy? Vzorec pro vztah mezi rychlostí, časem a vzdáleností. Úkoly a řešení.

Vzorec pro závislost času, rychlosti a vzdálenosti pro 4. ročník: jak se udává rychlost, čas, vzdálenost?

Lidé, zvířata nebo stroje se mohou pohybovat určitou rychlostí. Mohou jít určitou cestou v určitém čase. Například: dnes se do školy dostanete za půl hodiny. Jdete určitou rychlostí a 1000 metrů urazíte za 30 minut. V matematice se cesta, která je překonána, značí písmenemS. Rychlost se značí písmenem v. A dobu, po kterou je dráha projetá, označujeme písmenem t.

• Cesta —S
• Rychlost — v
• Čas —t

Pokud přijdete pozdě do školy, můžete stejnou cestu projet za 20 minut a zvýšit svou rychlost. To znamená, že stejnou dráhu lze absolvovat v různých časech a různou rychlostí.

Jak závisí doba jízdy na rychlosti?

Čím vyšší rychlost, tím rychlejší bude vzdálenost. A čím nižší rychlost, tím déle bude cesta trvat.

​​​​

Jak zjistit čas při znalosti rychlosti a vzdálenosti?

Abyste mohli zjistit dobu, kterou trvalo ujetí vzdálenosti, potřebujete znát vzdálenost a rychlost. Pokud vzdálenost vydělíte rychlostí, poznáte čas. Příklad takového úkolu:

Úkol o zajíci. Zajíc utíkal před Vlkem rychlostí 1 kilometr za minutu. Uběhl 3 kilometry ke své díře. Po nějaké době Hare běžel k díře?

Jak snadné je řešit pohybové problémy, kde potřebujete najít vzdálenost, čas nebo rychlost?

1. Přečtěte si pozorně problém a určete, co je známo ze stavu problému.
2. Zapište tyto údaje do návrhu.
3. Napište také, co je neznámé a co se má najít
4. Použijte vzorec pro problémy se vzdáleností, časem a rychlostí
5. Zadejte známá data ve vzorci a vyřešte úlohu

Řešení úlohy o zajíci a vlkovi.

• Ze stavu problému určíme, že známe rychlost a vzdálenost.
• Z podmínky problému také určíme, že potřebujeme najít čas, za který zajíc doběhnul k díře.

Tyto údaje zapisujeme například do návrhu:

Vzdálenost k díře — 3 kilometry

Rychlost zajíce — 1 kilometr za 1 minutu

Čas není znám

Nyní totéž zapišme matematickými symboly:

S— 3 kilometry

V — 1 km/min

t—?

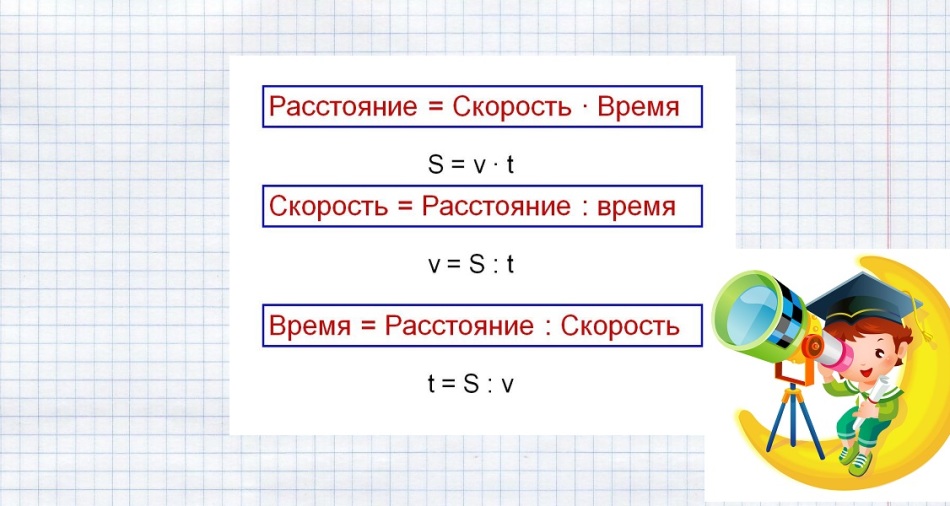
Vzpomeneme si a zapíšeme do sešitu vzorec pro hledání času:

t = S: v

Nyní zapíšeme řešení úlohy v číslech:

t = 3: 1 = 3 minuty

Jak zjistit rychlost, když je znám čas a vzdálenost?

Aby bylo možné zjistit rychlost, pokud je znám čas a vzdálenost, musí se vzdálenost vydělit časem. Příklad takového úkolu:

Zajíc utekl Vlkovi a běžel 3 kilometry k jeho noře. Tuto vzdálenost urazil za 3 minuty. Jak rychle zajíc běžel?

Řešení pohybové úlohy:

1. V návrhu napíšeme, že známe vzdálenost a čas.
2. Z podmínky úlohy určíme, že potřebujeme najít rychlost
3. Připomeneme si vzorec pro zjištění rychlosti.

Vzorce pro řešení takových problémů jsou zobrazeny na obrázku níže.

Dosaďte známá data a vyřešte úlohu:

Vzdálenost k díře je 3 kilometry

Doba, za kterou Zajíc dosáhl díry, byla 3 minuty

Rychlost není známa

Zapišme tato známá data do matematických symbolů

S— 3 kilometry

 t— 3 minuty

v —?

Napíšeme vzorec pro zjištění rychlosti

v = S: t

Nyní zapíšeme řešení úlohy v číslech:

v = 3: 3 = 1 km/min

Jak zjistit vzdálenost, pokud čas a rychlost je známa?

Chcete-li zjistit vzdálenost, pokud je znám čas a rychlost, vynásobte ji rychlostí. Příklad takového úkolu:

Zajíc utekl Vlkovi rychlostí 1 kilometr za 1 minutu. Trvalo mu tři minuty, než běžel k díře. Jak daleko Zajíc běžel?

Řešení úlohy: Do návrhu zapíšeme, co víme ze stavu úlohy:

Rychlost Zajíce je 1 kilometr za 1 minutu

Čas, kdy zajíc doběhl k díře - 3 minuty

Vzdálenost - neznámá

Nyní totéž zapišme matematickými symboly:

v — 1 km/min

t— 3 minuty

S —?

Připomeneme si vzorec pro zjištění vzdálenosti:

S = v ⋅ t

Nyní zapíšeme řešení úlohy v číslech:

S = 3 ⋅ 1 = 3 km

Jak se naučit řešit složitější úlohy?

Abyste se naučili řešit složitější úlohy, musíte pochopit, jak řešit jednoduché, zapamatovat si, které znaky označují vzdálenost, rychlost a čas. Pokud si nepamatujete matematické vzorce, zapište si je na kus papíru a mějte je při řešení úloh vždy po ruce. Vyřešte s dítětem jednoduché úkoly, které vymyslíte na cestách, například při procházce.

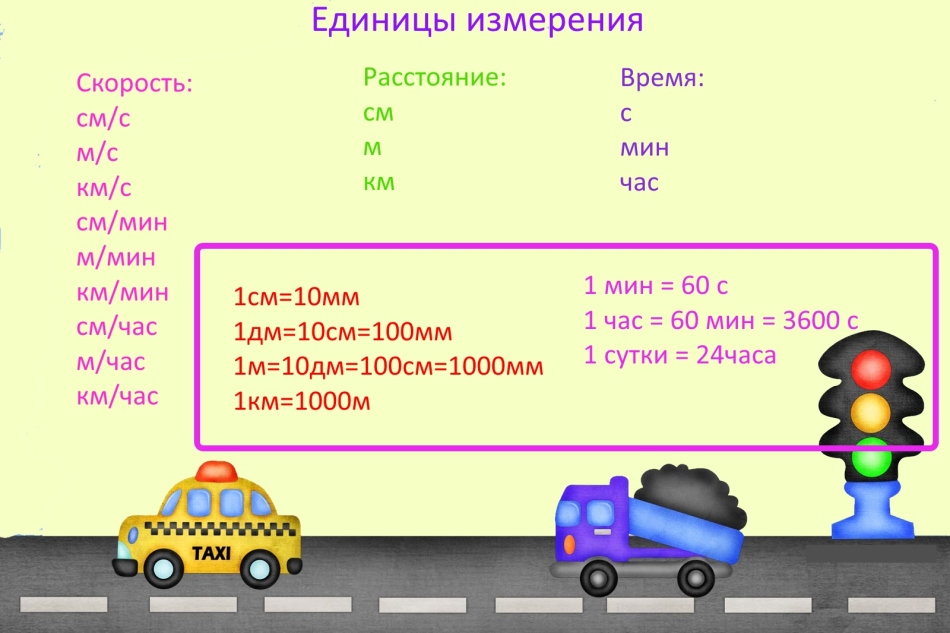
Jednotky měření

​​

Při řešení problémů o rychlosti, čase a vzdálenosti často dělají chybu, protože zapomínají převádět jednotky měření.

DŮLEŽITÉ: Jednotky měření mohou být libovolné, ale pokud ve stejném problému existují různé jednotky měření, převeďte je na stejné. Pokud je například rychlost měřena v kilometrech za minutu, musí být vzdálenost uvedena v kilometrech a čas v minutách.

Pro zvědavce : Obecně přijímaný systém měr se nazývá metrický, ale ne vždy tomu tak bylo a ve starověkém Rusku se používaly jiné měrné jednotky.

Problém s hroznýšem : Slůně a opice měřili délku boa v ​​krocích. Posunuli se k sobě. Rychlost opice byla 60 cm za sekundu a rychlost slůněte 20 cm za sekundu. Měřením strávili 5 sekund. Jaká je délka hroznýše? (řešení pod obrázkem)

> Řešení:

Z podmínek úlohy určíme, že známe rychlost opice a slůněte a čas, který potřebovali na změření délky hroznýše.

Zapišme si tyto údaje:

Rychlost opice je 60 cm/sec

Rychlost slůněte je 20 cm/s

Čas — 5 sekund

Vzdálenost neznámá

Tyto údaje zapišme matematickými symboly:

v1 — 60 cm/sec

v2 – 20 cm/s

t – 5 sekund

S —?

Zapišme si vzorec pro vzdálenost, pokud je známa rychlost a čas:

S = v ⋅ t

Spočítejme vzdálenost, kterou opice urazila:

S1 = 60 ⋅ 5 = 300 cm

Nyní spočítejme, jak daleko ušlo slůně:

S2 = 20 ⋅ 5 = 100 cm

Sečteme vzdálenost, kterou urazila opice a vzdálenost, kterou urazilo slůně:

S = S1 + S2 = 300 + 100 = 400 cm

Graf závislosti rychlosti těla na čase: foto

Vzdálenost pokryta různými rychlostmi je pokryta v různých časech. Čím vyšší rychlost, tím méně času trvá pohyb.

Tabulka 4 třída: rychlost, čas, vzdálenost

Č.	Rychlost (km/h)	Čas (hodina)	Vzdálenost (km)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Můžete fantazírovat a vymýšlet úkoly pro stůl sám. Níže jsou naše možnosti pro podmínky úkolů:

1. Maminka poslala Karkulku k babičce. Dívka byla neustále rozptylována a šla lesem pomalu, rychlostí 5 km/h. Na cestě strávila 2 hodiny. Jak daleko za tu dobu ušla Červená karkulka?
2. Pošťák Pechkin převážel balík na kole rychlostí 12 km/h. Ví, že vzdálenost mezi jeho domem a domem strýce Fedora je 12 km. Pomozte Pechkinovi spočítat, jak dlouho bude cesta trvat?
3. Papa Ksyusha si koupil auto a rozhodl se vzít rodinu k moři. Automobil jel rychlostí 60 km/h a na silnici strávil 4 hodiny. Jaká je vzdálenost mezi domem Ksyusha a pobřežím moře?
4. Kachny se shromáždily v klínu a odletěly do teplých krajů. Ptáci neúnavně mávali křídly po dobu 3 hodin a během této doby urazili 300 km. Jaká byla rychlost ptáků?
5. Letoun AN-2 letí rychlostí 220 km/h. Odstartoval z Moskvy a letí do Nižního Novgorodu, vzdálenost mezi těmito dvěma městy je 440 km. Jak dlouho bude letadlo na cestě?

Odpovědi na uvedené problémy naleznete v tabulce níže:

Č.	Rychlost (km/h))	Čas (hodina)	Vzdálenost (km)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Příklady řešení úloh rychlosti, času, vzdálenosti pro 4. ročník

Pokud je v jednom úkolu více pohybujících se objektů, musíte dítě naučit, aby pohyb těchto objektů zvažovalo samostatně a teprve potom společně. Příklad takového úkolu:

Dva přátelé Vadyk a Tema se rozhodli jít na procházku a opustili své domy, aby se setkali. Vadyk jel na kole a Tema šla. Vadyk jel rychlostí 10 km/h a Tema šel rychlostí 5 km/h. O hodinu později se setkali. Jaká je vzdálenost mezi Vadikovými a Teminými domy?

Tento problém lze vyřešit pomocí vzorce pro závislost vzdálenosti na rychlosti a času.

S = v ⋅ t

Vzdálenost, kterou Vadyk ujel na kole, se bude rovnat jeho vynásobené rychlosti podle času v tranzitu.

S = 10 ⋅ 1 = 10 kilometrů

Vzdálenost ujetá Subjektem se vypočítá podobně:

S = v ⋅ t

Dosaďte digitální hodnoty jeho rychlosti a času do vzorce

S = 5 ⋅ 1 = 5 kilometrů

Vzdálenost, kterou ujel Vadyk, je nutné přičíst ke vzdálenosti, kterou ujela Tema.

10 + 5 = 15 kilometrů

Jak se naučit řešit složité problémy, které vyžadují logické myšlení?

K rozvoji logického myšlení dítěte je nutné řešit z nich jednoduché, následně složité logické úlohy. Tyto úkoly se mohou skládat z několika fází. Z jedné fáze do druhé můžete přejít pouze v případě, že je vyřešena předchozí. Příklad takového úkolu:

Anton jel na kole rychlostí 12 km/h a Lisa jela na koloběžce rychlostí 2krát menší než Anton a Denis šel rychlostí 2x nižší než Lisa. Jakou rychlost má Denis?

K vyřešení tohoto problému musíte nejprve znát rychlost Lisy a teprve potom Denisovu rychlost.

Dva cyklisté odjeli z různých měst, aby se setkali. Jeden z nich spěchal a jel rychlostí 12 km/h a druhý jel v klidu rychlostí 8 km/h. Vzdálenost mezi městy, ze kterých cyklisté vyjížděli, je 60 km. Jak daleko každý cyklista urazí, než se setká? (řešení pod fotkou)

Řešení:

• 12+8 = 20 (km/h) je celková rychlost obou cyklistů nebo rychlost, kterou se k sobě přiblížili
• 60: 20 = 3 (h) je doba, po které se cyklisté setkali
• 3 ⋅ 8 = 24 (km) je vzdálenost ujetá prvním cyklistou
• 12 ⋅ 3 = 36 (km) je vzdálenost ujetá druhým cyklistou
• Kontrola: 36+24=60 (km) je vzdálenost ujetá dvěma cyklisty.
• Odpověď: 24 km, 36 km.

Nabídněte dětem řešení následujících úkolů formou hry. Možná si budou chtít udělat vlastní problém s přáteli, zvířaty nebo ptáky.

VIDEO: Problémy s pohybem