Oblast kruhu: vzorec. Proč je plocha kruhu popsána a vepsána do čtverce rovna pravoúhlému rovnoramennému trojúhelníku, pravoúhlému rovnoramennému lichoběžníku?

Jak najít oblast kruhu? Nejprve najděte poloměr. Naučte se řešit jednoduché i složité úkoly.

Kružnice je uzavřená křivka. Jakýkoli bod na kružnici bude stejně vzdálený od středu. Kruh je plochý tvar, takže řešení úkolu najít oblast je jednoduché. V tomto článku se podíváme na to, jak najít oblast kruhu vepsaného do trojúhelníku, lichoběžníku, čtverce a popsaného v blízkosti těchto obrázků.

Oblast kruhu: vzorec pomocí poloměru, průměru, délky kruhu, příklady řešení problémů

Najít obsah ​​číslo, musíte vědět, že takový je poloměr, průměr a číslo π.

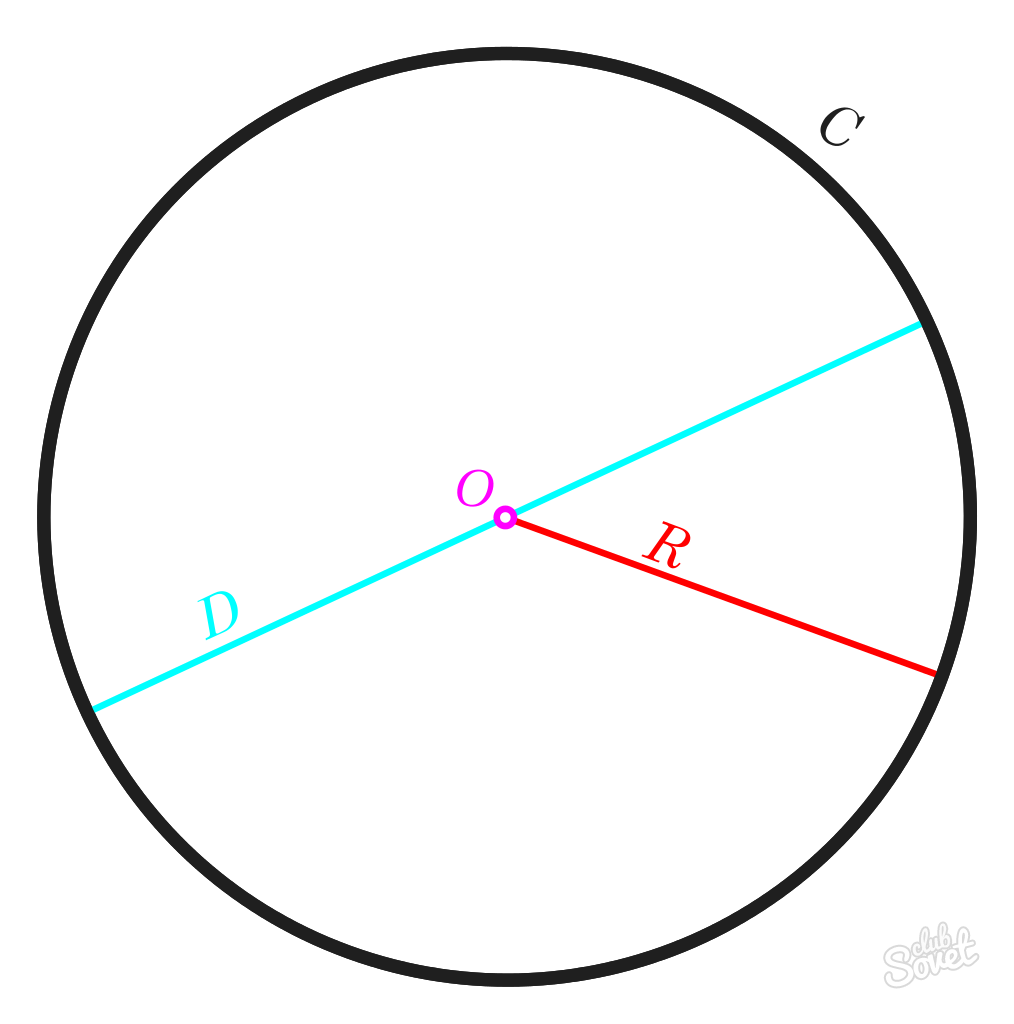
Poloměr R je vzdálenost ohraničená středem kružnice. Délky všech R-poloměrů jedné kružnice budou stejné.

Průměr D je přímka mezi libovolnými dvěma body na kružnici procházející středem. Délka tohoto segmentu se rovná délce poloměru R vynásobené 2.

Číslo π je konstantní hodnota rovna 3,1415926. V matematice se toto číslo obvykle zaokrouhluje nahoru na 3,14.

Vzorec pro zjištění obsahu kruhu přes poloměr:

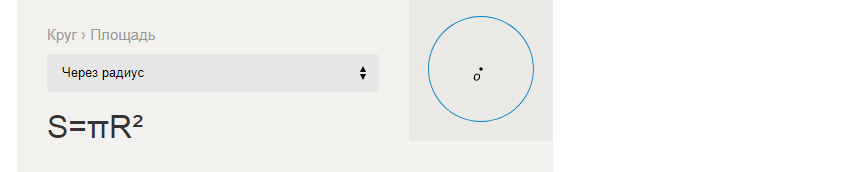
Příklady řešení úloh pro nalezení S-oblasti kruhu přes R-poloměr:

---------- ----------------------------- --

Úkol: Najděte obsah kruhu, je-li jeho poloměr 7 cm.

Řešení: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Odpověď: Plocha kruhu je 153,86 cm2.

Vzorec pro zjištění S-oblasti kruhu přes D-průměr:

Příklady řešení úloh na nalezení S, je-li D známo:

--------- --------------------------------

Úkol: Najděte S kruhu, je-li jeho D rovno 10 cm.

Řešení: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Odpověď: Plocha ploché kulaté postavy je 78,5 cm2.

Nalezení S kružnice, pokud je známa délka kružnice:

Nejprve zjistíme, jaký je poloměr. Délka kružnice se vypočítá podle vzorce: L=2πR, podle toho bude poloměr R roven L/2π. Nyní najdeme obsah kruhu pomocí vzorce až R.

Uvažujme řešení na příkladu úlohy:

----------- -----------------------------

Úkol: Najděte obsah kruhu, je-li známa délka kruhu L — 12 cm.

Řešení: Nejprve najdeme poloměr: R=L/2π=12/2*3,14=12/6,28=1,91.

Nyní najdeme plochu přes poloměr: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Odpověď: Plocha kruhu je 11,46 cm2.

Oblast kruhu vepsané do čtverce: vzorec, příklady řešení úloh

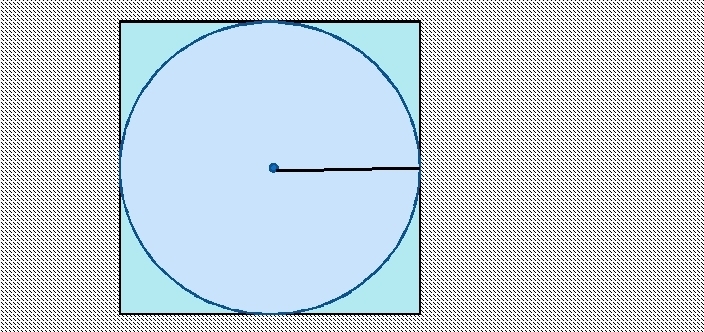
Nalezení obsahu kruhu vepsaného do čtverce je jednoduché. Strana čtverce je průměr kruhu. Chcete-li najít poloměr, musíte vydělit stranu 2.

Vzorec pro zjištění plochy kruhu vepsaného do čtverce:

Příklady řešení úloh pro nalezení oblasti kružnice vepsané v čtverec:

---------------------------------- ----

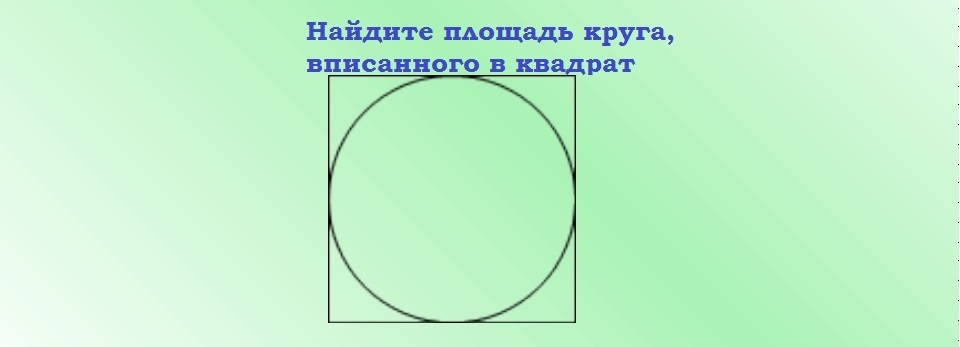
Úkol č. 1: Je známá strana čtvercového obrazce, která se rovná 6 centimetrům. Najděte S-oblast vepsaného kruhu.

Řešení: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Odpověď: Plocha ploché kulaté postavy je 28,26 cm2.

----------------------------------------- -----------

Úkol č. 2 :Najděte S kružnice vepsané do čtvercového obrazce a jeho poloměr, pokud je jedna strana rovna a=4 viz

Řešte následovně : Nejprve najdeme R=a/2=4/2=2 viz.

Nyní najdeme obsah kruhu S=3,14*22=3,14*4=12,56 cm2.

Odpověď: Plocha plochého kruhového obrazce je 12,56 cm2.

Oblast kružnice opsané čtverci: vzorec, příklady řešení úloh

Trochu obtížnější je najít oblast kulatého obrazce popsaného kolem čtverce. Ale pokud znáte vzorec, můžete tuto hodnotu rychle vypočítat.

Vzorec pro nalezení S kružnice opsané čtverci:

Příklady řešení úloh pro nalezení oblasti kruhu popsaného kolem čtvercového obrazce:

Úloha

Oblast kružnice vepsané do pravoúhlého a rovnoramenného trojúhelníku: vzorec, příklady řešení úloh

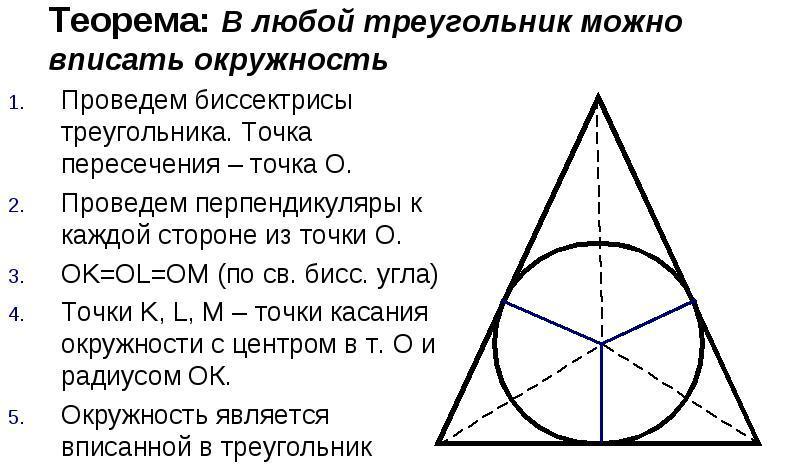
Kružnice vepsaná do trojúhelníkového obrazce je kružnice, která se dotýká všech tří stran trojúhelníku. Jakýkoli trojúhelníkový obrazec může být vepsán kruhem, ale pouze jedním. Střed kružnice bude průsečíkem osy úhlu trojúhelníku.

Vzorec pro zjištění obsahu kružnice vepsané do rovnoramenného trojúhelníku:

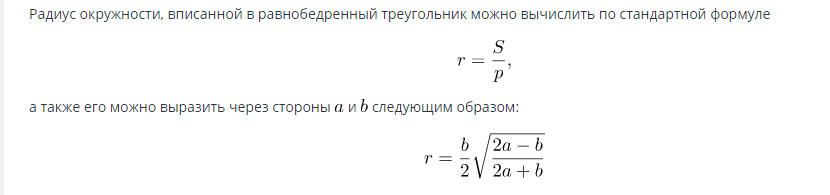
Když je známý poloměr, lze plochu vypočítat pomocí vzorce: S=πR2.

Vzorec pro zjištění obsahu kruhu vepsaného do pravoúhlého trojúhelníku:

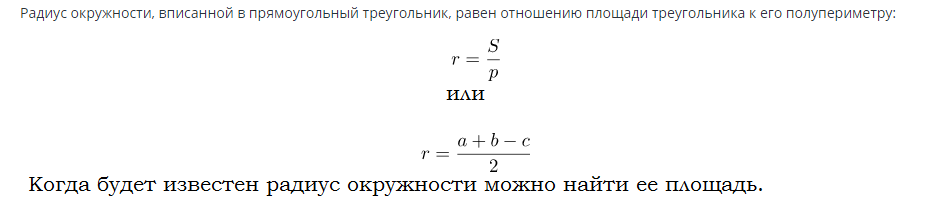
Příklady řešení úloh:

Úloha # 1

)

Pokud v tomto problému potřebujete také najít oblast kruhu o poloměru 4 cm, můžete to udělat podle vzorce: S=πR2

Úkol #2

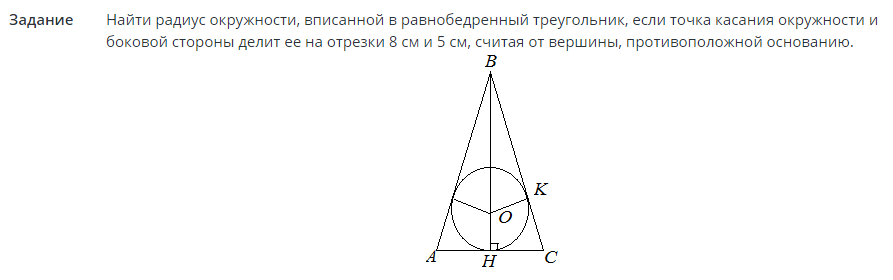
Řešení:

Nyní, když je poloměr znám, lze oblast kruhu nalézt z hlediska poloměru. Viz vzorec výše v textu.

Úkol #3

Oblast kružnice opsané pravoúhlému a rovnoramennému trojúhelníku: vzorec, příklady řešení úloh

Všechny vzorce pro nalezení oblasti kruhu se scvrkává na skutečnost, že nejprve musíte najít jeho poloměr. Když je znám poloměr, pak je nalezení oblasti jednoduché, jak je popsáno výše.

​​​​

Obsah kružnice opsané pravoúhlému a rovnoramennému trojúhelníku se zjistí podle následujícího vzorce:

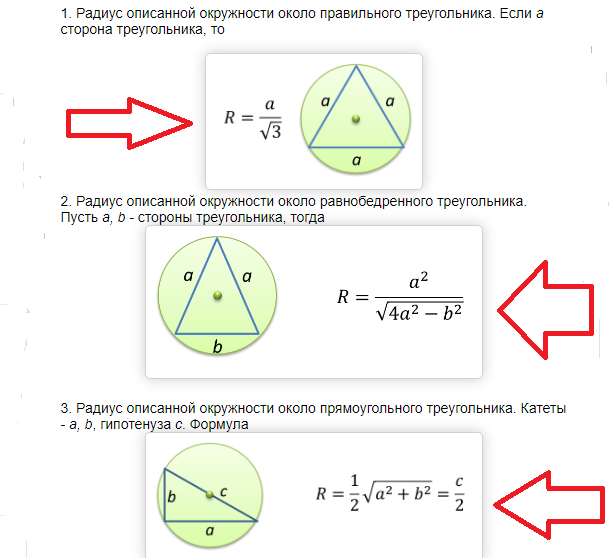
Příklady řešení problému:

Zde je další příklad řešení problém s použitím Heronova vzorce.

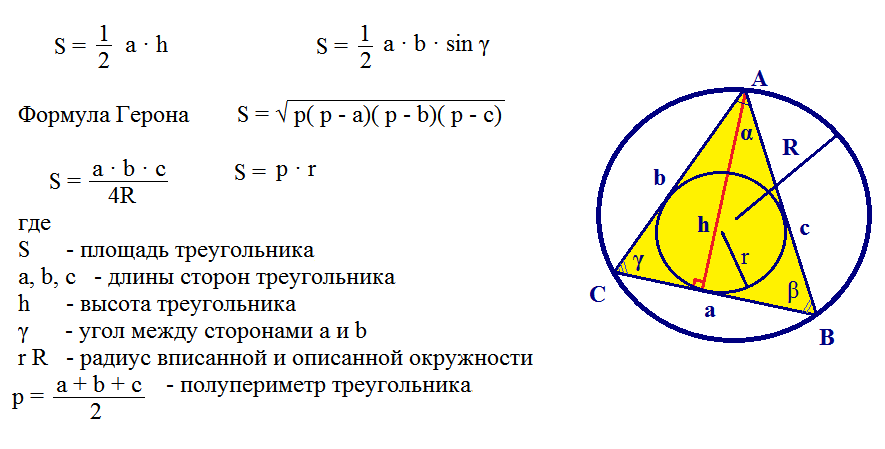
Je obtížné vyřešit podobné problémy, ale lze je překonat, pokud znáte všechny vzorce. Takové úlohy řeší žáci v 9. ročníku.

Plocha kružnice vepsané do pravoúhlého a rovnoramenného lichoběžníku: vzorec, příklady řešení problémů

Například rovnoramenný lichoběžník je vepsán kruh, který je v bodě dotyku, rozděluje jednu stranu na segmenty m a n.

K vyřešení tohoto problému je třeba použít následující vzorce:

Zjištění plochy kružnice vepsané do pravoúhlého lichoběžníku se provádí podle následujícího vzorce:

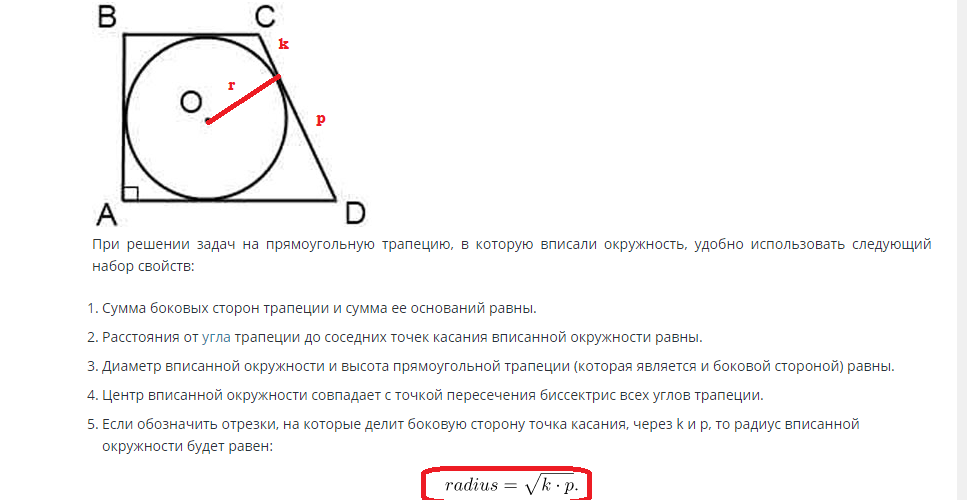
Je-li známá strana, pak lze poloměr zjistit prostřednictvím této hodnoty. Výška strany lichoběžníku se rovná průměru kružnice a poloměr je polovina průměru. V souladu s tím je poloměr roven R=d/2.

Příklady řešení úloh:

Oblast kružnice opsané kolem pravoúhlého a rovnoramenného lichoběžníku: vzorec, příklady řešení problémů

Lichoběžník lze vepsat v kruhu, když součet protilehlých úhlů je 180°. Proto lze vepsat pouze rovnostranný lichoběžník. Poloměr pro výpočet plochy kruhu popsaného v blízkosti pravoúhlého nebo rovnoramenného lichoběžníku se vypočítá pomocí následujících vzorců:

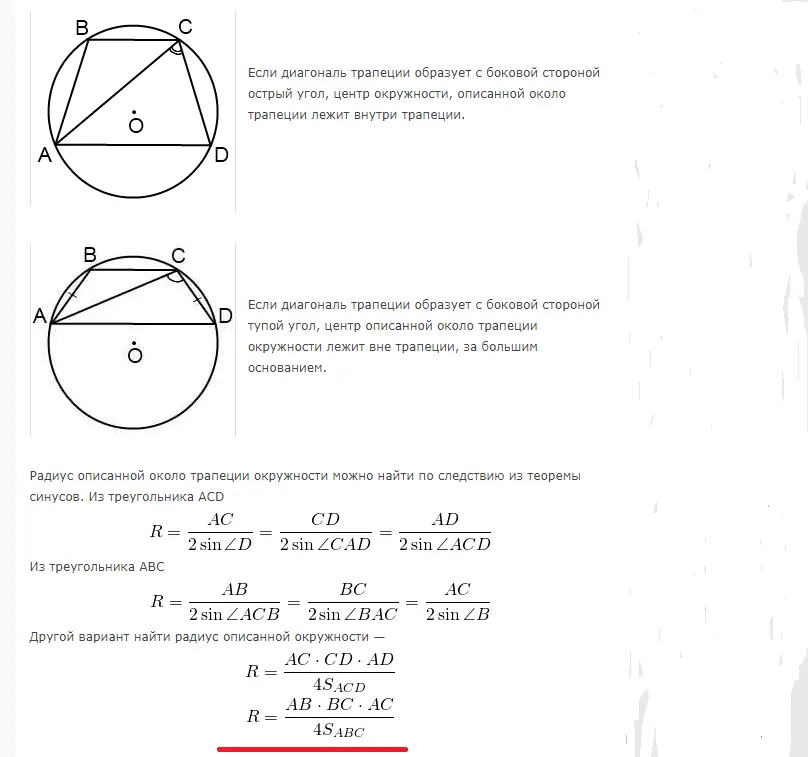
Příklady řešení problémů:

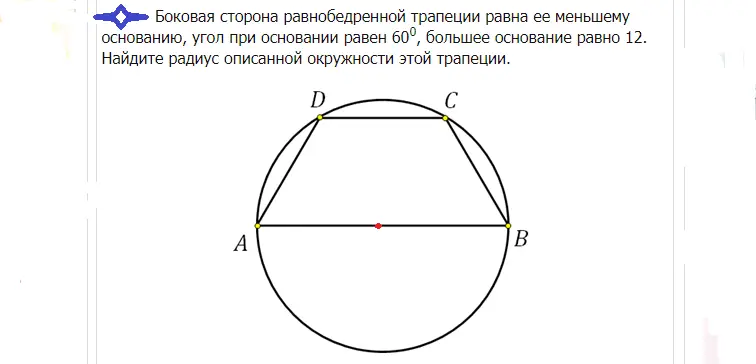
Řešení: Velká základna v tomto případě prochází středem, protože do kruhu je vepsán rovnoramenný lichoběžník. Střed rozděluje tuto základnu přesně na polovinu. Pokud je základna AB rovna 12, pak poloměr R lze nalézt následovně: R=12/2=6.

Odpověď: Poloměr je 6.

V geometrii je důležité znát vzorce. Nelze si je ale všechny zapamatovat, takže i na mnoha zkouškách je povoleno používat speciální formulář. Je však důležité umět najít správný vzorec pro řešení toho či onoho problému. Procvičte si řešení různých problémů pro nalezení poloměru a oblasti kruhu, abyste mohli správně nahradit vzorce a získat přesné odpovědi.

Video: Matematika | Výpočet ploch kružnice a jejích částí